Dot Product: A vector is a amount that has each value (numerical size) AND path. A scalar, on the opposite hand, is a amount that has most effective value – it is only a wide variety. Vectors are such things as speed, displacement, pressure, or electric powered field. Those portions continually have a path. A speed is not three m/s; it is three m/s NORTH. But a scalar might be some thing like temperature, time or distance. Those are described through their numerical values – they may be now no longer pointed in any unique path.
When we multiply numbers collectively that occur to be vectors, we do it in extraordinary approaches relying at the circumstances. If the end result you may be getting is a vector amount – if it has a path itself – then you need to do a move product. But if the end result you need is a scalar amount, a amount that does not have a path, you then definitely use a dot product. A dot product is in which you multiply one vector through the thing of the second one vector, which acts within side the path of the primary vector.
So, for instance, paintings is pressure increased through displacement. It’s vectors increased collectively. But extra mainly it is the pressure performing within side the path you are moving, increased through the displacement. This is why paintings is a dot product. Of course, the truth that paintings is a scalar amount, now no longer a vector, may additionally have tipped you off.
Dot Product Formula
The dot product approach the scalar manufactured from vectors. It is a scalar wide variety acquired through acting a selected operation at the vector additives. The dot product is relevant most effective for pairs of vectors having the identical wide variety of dimensions. The image used for the dot product is a heavy dot. This dot product is appreciably in arithmetic in addition to in Physics. This article will provide an explanation for the dot product formulation with examples. Let us research it!
Dot Product
The idea of dot product says that vectors may be increased for buying the scalar amount. It is used for buying the product. It is giving the goods of or extra vectors in or extra dimensions.
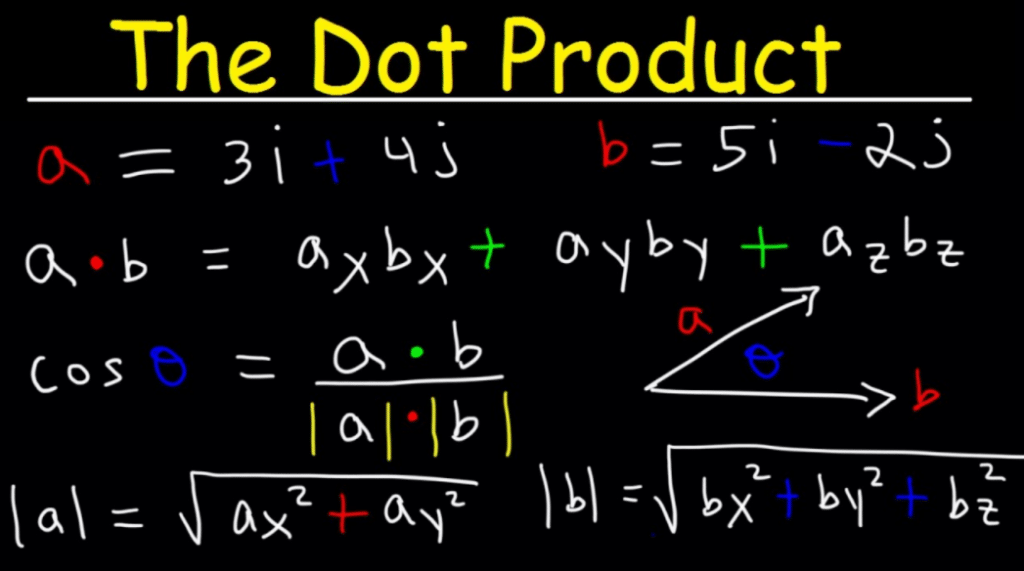
The geometric definition of the dot product says that the dot product among vectors a and b is given as is the attitude among vectors a and b. Although this formulation is properly used for expertise the homes of the dot product. A formulation for the dot product in phrases of the vector additives will make it less complicated to calculate the dot product among given vectors.
Equations for Dot Product
There are equations for dot products. One for if you have the general magnitudes and angles of the vector, which seems like this: And another, in case you’re given the 2 vectors in thing form, which seems like this: Dot product equation: thing form dot product equation So, for the primary, in case you’re multiplying vector A and vector B collectively, you are taking the value of vector A, multiply it through the value of vector B, and multiply that through the cosine of the attitude among them.
Read Also: Gravitational Pull of the Earth: Definition & Overview
But for the second one equation, a scenario which you do not know the general magnitudes, you multiply the x additives and y additives collectively one by one after which upload them up. The solution works out precisely the identical. So, with our instance of paintings, in case your recognize that the pressure is three newtons and the displacement is two meters and the attitude
among the pressure and displacement is 30 degrees, you multiply three through 2 through cosine 30 and also you get your solution. But, if as an alternative you are advised that the pressure is 30i + 8j newtons, and the displacement is 15i + 15j meters, you’ll as an alternative use the second one equation. It’s all primarily based totally on what records you are given.
Example Calculations
Alright, let’s undergo an instance. Imagine you are sweeping the ground with a broom. You’re pushing down at the broom with a pressure of fifty newtons. Hence, the broom is at a 50 diploma attitude with the ground. So you are pushing partially down and partially forwards. If you push the broom three meters throughout the ground, how plenty paintings completes?
Well, paintings is a scalar and is identical to pressure increased through displacement, so we surely need to do a dot product (I’m positive you are very surprised). First of all, let’s write out what we recognize. The pressure, F, is 50 newtons and the displacement, x, is three meters.
Read Also: Thermoreceptors: Definition & Function
Looking at this diagram, we will see that the attitude among the pressure and the displacement is similar to the attitude among the broom and the ground – 50 degrees. So theta equals 50 degrees. Plug all that into our product equation, and we get 50 increase through three increased through cosine 50. It offers us 96.four Joules of paintings. And it’s it; it’s our solution.
Dot Product Formula
To create mastery in mathematics, you must recognize that specific points are the same and vary in the name we provide. Thus, the case with portions, percents, decimals, fundamental level, vectors, complex numbers, and factors on an advanced degree. We look at these last three and discuss them in a little bit of information.
The majority of trainees learn more about factors and the Cartesian plane– the grid on which we outline them– by the sixth grade. On a graph, the upright axis is called the y-axis (ordinate), and the horizontal is called the x-axis (abscissa). Points are provided as two numbers in parentheses, separated by a comma. Hence the end (1, 4) or (-2, 5). To locate the first factor, from the origin or 0. We look at the appropriate one on the straight and up to four on the upright and place the element.
Vector Dot Product Formula: Final Thoughts
To graph the second, we go to the left two units from the origin and up 5. It should be clear that the initial number in parentheses corresponds to the x-coordinate and the 2nd to the y-coordinate. Additionally, for the x-coordinates, unfavourable means we position to the left and positive to the right. Also, for the y-coordinates, damaging methods we position down and also positive up.