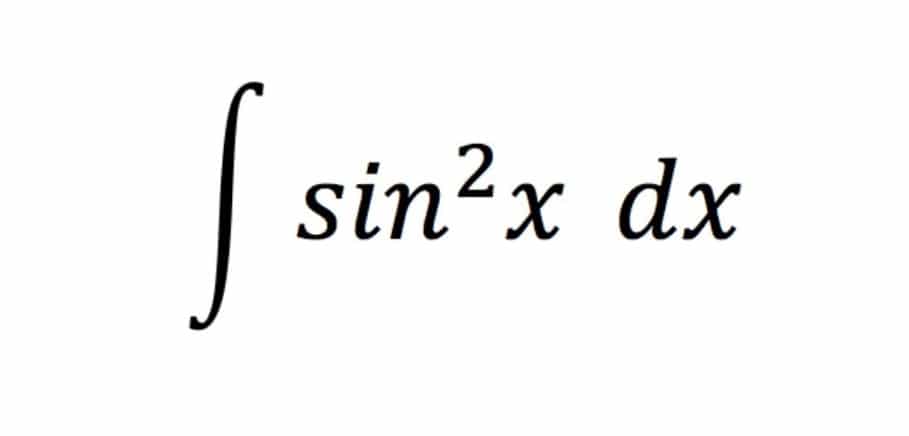Throughout high school, integration has been one of the most dreaded topics in Mathematics.
This article explains the integral of sin2(x) in detail.
Actually, the topics of Integration and differentiation go hand-in-hand.
The word ‘integration’ means ‘to integrate’, that is, ‘to join’.
Differentiation means to break down a function into infinitesimal small parts. On the contrary, integration is just the reverse. Actually, it requires joining these infinitesimally small parts to form the original function.

Integral of ∫sin2(X)
For the integral of sin2(x), the integration function can be written as:
I = ∫sin2(x) dx ____(1)
Clearly, we cannot solve this integral using any direct formula. So, in order to solve this, we have to use the trigonometric identity of the half angle ∫sin2(x).
Now, as we all know, the trigonometric identity of the half angle sin2(x) = (1 – cos 2x) / 2.
Thus, equation____(1) can be rewritten as:
I = ∫ (1 – cos 2x) / 2 dx,
Or, I = 1/2 ( ∫ (1 – cos 2x) dx,
Or, I = 1/2 ∫ 1 dx – 1/2 ∫ cos 2x dx,
Hence, the first part of the integral is very easily solvable. But, for the second part of the integral, we need to apply an integration formula.
Also, we have to use the integration formula:
∫ cos kx dx= (sin kx / k) + c.
Further, using this formula, we have,
∫ sin2(x) dx = x / 2 – 1 / 2 * (sin 2x) / 2 + c,
Or, ∫sin2(x) dx = x / 2 – 1 / 4 * (sin 2x) + c,
( where, ‘c’ is a constant ).
Thus, it is clear that the integral of sin2(x) is x / 2 – 1 / 4 * (sin 2x) + c.
Integral of ∫ sin2(x) dx steps explained
We have to integrate ∫ sin2(x) dx. Further, we have broken down the steps of the integral of sin2(x) for you to understand better.
For sin2(x), we will use the cos double angle formula:
cos(2x) = 1 – 2 sin2(x)
Now, the above formula can be rearranged to make sin2(x) the subject:
sin2(x) = 1/2(1 – cos(2x))
You can now rewrite the integration:
∫sin2(x) dx = ∫ 1 / 2(1 – cos(2x)) dx
Then, we are using the sum rule( distributive rule)
∫ f(x) + g(x) dx= ∫ f(x) dx + ∫ g(x) dx.
Thus, we get ∫ (1 / 2) dx − ∫ ( cos 2x/2 ) dx.
Then, we use the ‘integration of constant’ rule:
∫ a dx = ax + c ; where ‘c’ is a constant.
Since 1/2 is a constant, we can remove it from the integration to make the calculation simpler. Therefore, we will get x / 2 − ∫ ( cos 2x) / 2 dx.
Following this, we can use the constant rule:
∫ a f(x) dx = a ∫ f(x) dx.
1 / 2 x ∫(1 – cos(2x)) dx = 1/2 x (x – 1/2sin(2x)) + C
Actually, it is very important that as this is not a definite integral, we must add the constant C at the end of the integration.
Now, simplifying the above equation gives us a final answer:
∫sin2(x) dx = 1 / 2X – 1 / 4 sin(2x) + C.
Now, let us find the integral of sin2(x) by using another method.
Integral of ∫ sin2(x) dx by parts
Let us now find the integral of ∫sin2(X) dx following the by parts method.
However, we shall use this formula for the same:
∫ 𝑢′(𝑥) 𝑣(𝑥) 𝑑𝑥 = 𝑢(𝑥) 𝑣(𝑥)−∫ 𝑢(𝑥) 𝑣′(𝑥) 𝑑𝑥
For this method, write ∫ sin2(x) dx as ∫ sin(x) sin(x) dx.
∫ sin(𝑥) sin(𝑥) 𝑑𝑥 = −cos(𝑥) sin(𝑥) − ∫ (−cos(𝑥)) cos(𝑥) 𝑑𝑥
If we apply integration by parts to the rightmost expression again, we will get,
∫ sin2(x) dx = ∫ sin2(x) dx, which is not very useful.
However, the real trick is to rewrite the ∫cos2(x) dx in the second step as 1− ∫ sin2(x) .
Then we get ∫ sin2(x)dx.
Now, all we have to do is to transfer ∫sin2(x) dx from the right-hand side to the left-hand side of the equation:
2 ∫sin2(x) dx = − cos(𝑥) sin(𝑥) + 𝑥 + 𝐶
∫sin2(x) dx = 1 / 2 (𝑥 − cos(𝑥) sin(𝑥)) + 𝐶____(2).
We know that sin 2x = 2 sin(x) cos(x).
Therefore, cos(x) sin(x) = (sin 2x) / 2.
So, if we substitute this value of cos(x) sin(x) in equation ___(2),
We will get:
∫ sin2(x) dx = x / 2 – (sin 2x) / 4 + C.
So, we should write C/2 rather than C, but it is still just an indefinite constant, so, as is customary, we rename C / 2 to C to get the result in the usual form.
Integral of sin2(x) from 0 to pi
As we have discussed a little later: there are two types of integration- definite and indefinite.
Now, we will move on to find the definite integral of sin2(x) when the upper limit(b) = π and the lower limit(a) = 0.
Solve the integral I = ∫sin2(x) dx over 0 to π.
So, this can be written as:
I = ∫sin2(x) dx over 0 to π
Further, we can simply write this as :
∫sin2(x) dx over 0 to π = ∫(1−cos2x) / 2) dx over 0 to π.
However, this is written because ( ∵ sin2(x) = (1−cos 2x) / 2).
= 1 / 2 [∫dx over 0 to π – ∫cos ( 2x ) dx over 0 to π]
= 1 / 2 [ x− (sin 2x) / 2
= 1 / 2 [ (π −0) − (sin 2π − sin 0) / 2]
= π / 2.
Thus, the definite integral of ∫ sin2(x) dx over the limits 0 to π is π / 2.
Integral of sin2(x) Wolfram:
Wolfram is yet another online calculator that calculates the integral of functions. So, obviously you can find the integral of sin2(x) on it as well.
The wolfram calculator is an exceptionally good one. This is because it not only displays the result with ease, but also displays the graph. It even displays the expanded form, alternate form, and the series expansion of the integral.
To summarize, it can be a really helpful tool for all students who wish to delve deep into a particular integral and find out its nature in detail.
Here, we are also providing the link for you to access this wonderful calculator:
Wolfram
Types of Integration:
We can classify integration into two types:
- Definite Integral.
- Indefinite integral.
- The first type of integral is the definite integral.

It is basically the integration over a fixed limit. Initially, two boundaries of the limit are given – the upper limit and the lower limit.
The number “a” that is at the bottom of the integral sign is called the lower limit of the integral and the number “b” at the top of the integral sign is called the upper limit of the integral. Also, despite the fact that a and b were given as an interval the lower limit does not necessarily need to be smaller than the upper limit. Collectively we’ll often call a and b the interval of integration.
Further, the rules for solving definite integrals are provided below:
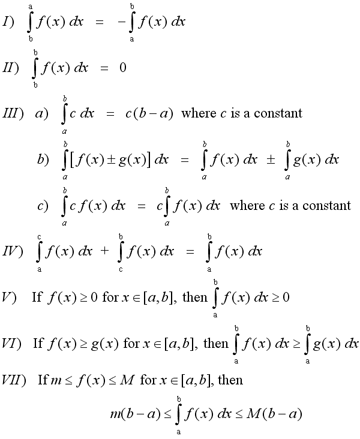
- Moving on, the second type of integrals are the indefinite integrals.

An indefinite integral, sometimes called an antiderivative, of a function f(x), denoted by
∫ f(x) dx is a function the derivative of which is f(x). Since the derivative of a constant is zero, the indefinite integral is not unique. However, the process of finding an indefinite integral is called integration.
Integral of sin 2x:
We can denote integral of sin 2x as:
∫ sin (2x) dx_____( 3)
However, this integration can be solved very easily. You can use the substitution method of integration to solve this.
Also, the value of this will be -(cos 2x) / 2 + C, where ‘C’ is the constant of integration.
Now, proceeding with the integration by substitution,
Now, assume 2x = u.
Totally differentiating,
2 dx = du.
Therefore, dx = du / 2.
Now, we have to substitute this value of dx in the integral of sin 2x, that is,
equation ___(3), we get,
∫ sin 2x dx = ∫ sin u (du/2)
= (1/2) ∫ sin u du
However, we know that the integral of sin x is -cos x + C. So, the last line can be written as:
= (1/2) [(-cos u) + C].
Now, substituting u = 2x back here,
∫ sin 2x dx = -(cos 2x) / 2 + C1, where C1 = C / 2.
So, this is the integral of the sin 2x formula.

Integral of sin2(x) FAQs:
1. What does sin2(x) integrate to?
Ans: The integral of sin2x is x / 2 – (sin 2x) / 4 + c.
2. Why is writing the constant of integration important in the indefinite integral of sin2(x)?
Ans: If F(x) is an antiderivative of a function f(x), that is, F'(x)= f(x),
Then G(x) = F(x) + C (where C is any constant) is also an antiderivative of f(x),
Since G'(x) = [F(x) + C]’= F'(x) = f(x).
Hence, there is a family of functions (only differ by a constant) that are antiderivatives of f(x). So, in order to include all antiderivatives of f(x), the constant of integration C is used for indefinite integrals. The importance of C is that it allows us to express the general form of antiderivatives.
3. Why is writing the constant of integration not important in the definite integral of sin2(x)?
Ans: In general, the form of a definite integral is:

Actually, the value of the definite integral of a function on [ a, b] is the difference of any antiderivative of the function evaluated at the upper limit of integration minus the same antiderivative evaluated at the lower limit of integration. Since the constants of integration are the same for both parts of this difference, they are ignored in the evaluation of the definite integral because they subtract and yield zero. Moving on and keeping this in mind, choose the constant of integration to be zero for all definite integrals.
4. What is the basic idea of integral calculus?
Ans: The basic idea of Integral calculus is finding the area under a curve.
So, to find it exactly, we can divide the area into infinite rectangles of infinitely small width and sum their areas. Thus, integral calculus is mainly used to deal with an infinite amount of things.