The rate of change implies the change in one variable with reference to the change in another variable. You have often calculated the rate of change in the context of mathematics or physics.

In this article, we will explain the need for the rate of change calculator. In addition, also explain the applications of the rate of change.
Rate of change formula:
The rate of change formula is used to find the rate of change of two variables. You just need to know the initial and the final values for the two variables.
Consider two variables x and y.
Assume, the initial value of y is y1 and the final value of y is y2.
Similarly, the initial value of x is x1 and the final value of x is x2.
Thus, the formula for finding the rate of change is:
Rate of change (r) = (y2 – y1) / (x2 – x1).
Basically, we divide the change in the output value by the change in the input value.
For a linear function, the rate of change m is represented in the slope-intercept form for a line: y=mx+b whereas the rate of change of functions is otherwise defined as, (f(b)-f(a))/ b-a.
Rate of change calculator
The rate of change calculator is a simple online tool that is used to find the rate of change in the explained variable (y) with reference to the explanatory variable (x).

The calculator has the following advantages:
- The calculator provides very accurate results.
- The rate of change calculator is pretty easily available.
- Additionally, it is not at all time consuming, as compared to the
pen-and-paper-based method.
- Also, you do not need to know the rate of change formula for using the
Rate of change calculator.
Rate of change calculator with steps
Remember, the rate of change calculator is a free online tool that gives the change in slope for the given input coordinate points.
Actually, it is pretty simple to use the rate of change calculator. Follow the steps given below and you will be able to obtain the results very easily:
Firstly, you have to realize that the rate of change is actually the slope of a line.
Secondly, put in the values of all the coefficients, The coefficients are x1, x2, y1 and, y2. You have to know the values of each of them.
Thirdly, once you are done plugging in the value of the variables, click on the ‘calculate’ button.
Finally, the output box will display the result.
So, you can see that the rate of change calculator makes the method of finding the rate of change very easy. In fact, you obtain the result in just a fraction of a few seconds.
Below, we have provided a link for a rate of change calculator:
Rate of change calculator at a point
Now, you might also be asked to find the rate of change at a point. This actually means the instantaneous rate of change.
The instantaneous rate of change refers to the change that takes place in a particular instant. It is actually equivalent to the value of the derivative, at a particular point.
For a graph, the instantaneous rate of change at a specific point is the same as the tangent line slope. That is, it is a curve’s slope.
The Formula of Instantaneous Rate of Change represented with limit looks like,

It is easy to use the rate of change at a point calculator.
It is provided below:
Further, we are explaining the steps you need to follow to derive accurate results using this calculator.
Firstly, enter the function for which you wish to calculate the rate of change at a point.
Secondly, enter the value of the point at which you want to find the rate of change.
Thirdly, click on the ‘Find instantaneous rate of change’ button.
Finally, the output box will display the instantaneous rate of change of the provided function at the specified point.
Thus, the ‘rate of change at a point’ calculator will make the calculations a lot easier for all.
Rate of change calculator with function
The rate of change calculator can also be used to find the results when you know the value of the function at that point. Say, you know the value of a variable( coordinate ) x1. At the same time, you have also been provided the function f(x). So, if you put the value of x1 in this function, then you obtain the value of f(x1).
Similarly, you might also know the value of x2. Putting this value of x2 in the function f(x), you will be able to find f(x2).
In totality, you know the values of x1, x2, f(x1), f(x2).
So, using these informations, we can calculate the rate of change(r) as:
[f(x2) – f(x1)] / [x2 – x1].
You can use this rate of change calculator if you only know the values of x1, x2, f(x1) and, f(x2).
calculator
Follow these steps to calculate the rate of change using this calculator:
Step-1: You know the values of x1, x2, f(x1) and, f(x2).
Plug in these values in the respective fields provided.
Step-2: Once you are done putting in the values, the average rate of change between the
two points of the same function is automatically displayed in the output box.
As you can see, using this calculator is that simple!
Rate of change calculator with table:
Suppose, for a given set of values of x, the corresponding values of y are given as below:
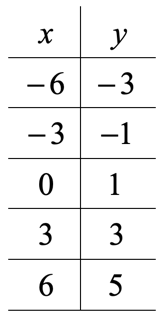
In order to find the rate of change at each point, you have to subtract two successive values of y and divide it by the difference of the two corresponding values of x.
For example, in the second step,
Change in y = -1 – (-3) = 2 and,
Change in x = -3 – (-6) = 3.
Thus, in this case, the rate of change will be 2 / 3.
If you want to use the calculator for performing the above calculation,
Put the first value of y in the f(x1) column and put the corresponding value of x in the provided space.
Similarly, put the next value of y in the f(x2) column and the corresponding value of x in the ‘x’ column.
The value of the rate of change, in this case, can be calculated with ease.
Also, it can be calculated for any two successive x-y values.
Rate of change applications
Often, we are asked to calculate the rate of change in the context of either Science or mathematics.
The rate of change (ROC) is the speed at which a variable changes over a specific period of time. ROC is often used when speaking about momentum, and it can generally be expressed as a ratio between a change in one variable relative to a corresponding change in another; graphically, the rate of change is represented by the slope of a line.
Moreover, other than the analytical application of derivatives, there is a ton of other real-life applications of differential calculus, without which many scientific proofs could not have been arrived at.
The rate of change is definitely one of them.
Rate of Change of Quantities
One of the most common applications of the rate of change calculator is to find the rate of change of quantities. In mathematics, if we have a dependent variable y and an independent variable x, then we need to find the rate of change of y due to a change in x.
Since y is the dependent variable, it means that a change in x is sure to have an effect on the value of y.
The rate of change calculates the exact change in y due to a change in x.
It is denoted by (dy / dx).
Also, the value of dy / dx gives us the exact change in y due to a unit change in x.
If the value of dy / dx is negative, that implies that an unit increase in x will lead to a decrease in the value of y.
On the contrary, if the value of dy / dx is positive, it means that a unit increase in x will increase the value of y.
If y = f(x),
f ’(x) = dy / dx is the rate of change of y due to a change in x.
Rate of change of momentum:
The rate of change of momentum of an object is directly proportional to the resultant force applied and is in the direction of the resultant force. In fact, the resultant force is equal to the rate of change of momentum.
momentum = mass * velocity
Differentiating both sides leads to,
force = mass * acceleration
since the mass doesn’t participate in the differentiation as it is constant.
The relationship between the force on an object and the rate of change of its momentum; valid only if the force is constant.
It is given as:
Change in momentum, Δp=Δ(mv)
However,
Rate of change of momentum = mass × acceleration
Or,
Δp / Δt = m * a = Force.
Rate of change of velocity
Similarly, the rate of change of velocity gives us the acceleration of an object.
Velocity is a vector quantity and so it has both magnitude and direction.
So, acceleration is a vector quantity as well.
Since the rate of change of velocity is called acceleration. Therefore the slope of any velocity – time graph will give the acceleration of the body.

Rate of change calculator calculus
Solved Examples:
- Find the average rate of change of the function y=2 e^(x) over the interval from x=0 to x=2.
Solution:
The average rate of change will be:
[f(2)−f(0)] / [2−0].
So, f(2) = 2 e^(2) and f(0) = 2 e^(0) = 2 * 1 = 2.
Therefore, the rate of change over x = [0,2] is:
[f(2)−f(0)] / [2−0]
Or, [2 e^(2) – 2] / [2 – 0]
Or, 2 [e^(2) – 1] / 2
Or, e^(2) – 1.
Thus, the answer will be e^(2) – 1.
2) Let us define a function as f(x) = −ln(x+1).
Find the average rate of change of the function over [0,4].
Solution:
We use the average rate of change formula, which gives us:
[f(4) – f(0)] / [4 – 0].
Now f(4) = −ln (4+1) = – ln 5, and
f(0) = −ln(0+1) = −ln1 = 0.
Therefore, the answer becomes:
[− ln5 − 0] / [4−0] = – ln 5 / 4.
3) Suppose we can model the profit, P, in dollars from selling x items with the
equation P(x) = 3x^2 − 4x + 2.
Find the average rate of change of the profit from x = 1 to x = 4.
Solution:
We need to apply the formula for the average rate of change to our
profit equation. Thus we find the average rate of change is:
[P(4) – P(1)] / [4 – 1].
Since P(4) = 3(4)^2 − 4(4) + 2 = 3(16) − 16 + 2 = 48 − 16 + 2 = 34
And,
P(1) = 3(1)^2 − 4(1) +2 = 3(1) − 4 + 2 = 3 − 4 + 2 = 1,
We find that the average rate of change is:
[34 – 1] / [4 – 1] = 33 / 3 = 11.
What are the examples of rate of change?
Knowingly or unknowingly, we come across applications of rate of change in almost every single instance in our day-to-day lives.
For example, a car traveling 68 miles per hour (distance traveled changes by 68 miles each hour as time passes) or,
A car driving 27 miles per gallon of gasoline (distance traveled changes by 27 miles for each gallon) and also,
The amount of money in a college account decreases by $4,000 per quarter.
Rate of change calculator FAQs
How do you interpret the rate of change according to the results provided by the rate of change calculator?
The rate of change of a linear function is the slope of the line it represents. It is the change in the values of f(x) per a one-unit increase in the values of x. A positive rate of change indicates that a linear function is increasing. On the contrary, a negative rate of change indicates that a linear function is decreasing.
Can we use the rate of change calculator only when we know the values of x1, x2, f(x1) and f(x2) ?
Yes, when the value of the function at specified points is given you can easily use the rate of change calculator for this.
You just have to plug in the values in the respective spaces for x1, x2, f(x1) and f(x2). Then, the output box will display the result. It will calculate the rate of change using the formula: [f(x2) – f(x1)] / [x2 – x1]. However, it is the same as the formula for finding the slope of a linear function.
The calculator for calculating the same is also provided above.
Is the rate of change calculator easy to use?
Yes, the rate of change calculator is actually very easy to use. You need not know any prior formula for calculating the rate of change using this. Simply, put in the equation and specify the point at which you want to calculate the rate of change.
The calculator will do the rest of the job for you.
How can I calculate the rate of change?
Simply explaining, to find the average rate of change, we divide the change in the output value by the change in the input value.
You can either perform this calculation manually or you can also use the rate of change calculator available online.
What is the rate of change in calculus?
The average rate of change of the function f over that same interval is the ratio of the amount of change over that interval to the corresponding change in the x values. It is given by [f ( a + h ) − f ( a )] / h .
We have also discussed this in our article above.





