The angles created when a transversal intersects two coplanar lines are popular as alternative interior angles. They are on the inside of the parallel lines but the outside of the transversal. The transversal also cuts through two lines that are Coplanar at different places. These angles indicate whether or not the two provided lines are parallel. If these angles are equivalent, the lines intersecting with the transversal are parallel.
An angle is produced when two rays, or lines with just one terminus, intersect at a point known as a vertex. The distance between the two beams determines the angle. Angles in geometry are frequently represented using the angle symbol. Thus angle A might be written as angle A, or When a line (present there as a transversal) crosses two lines, AIAs develop on opposing sides of the transversal. Now, if the two lines are parallel, then the alternate interior angles are equal. If you want to know more about this topic, you’re welcome here. Read on as we describe how Alternate Interior Angles work.
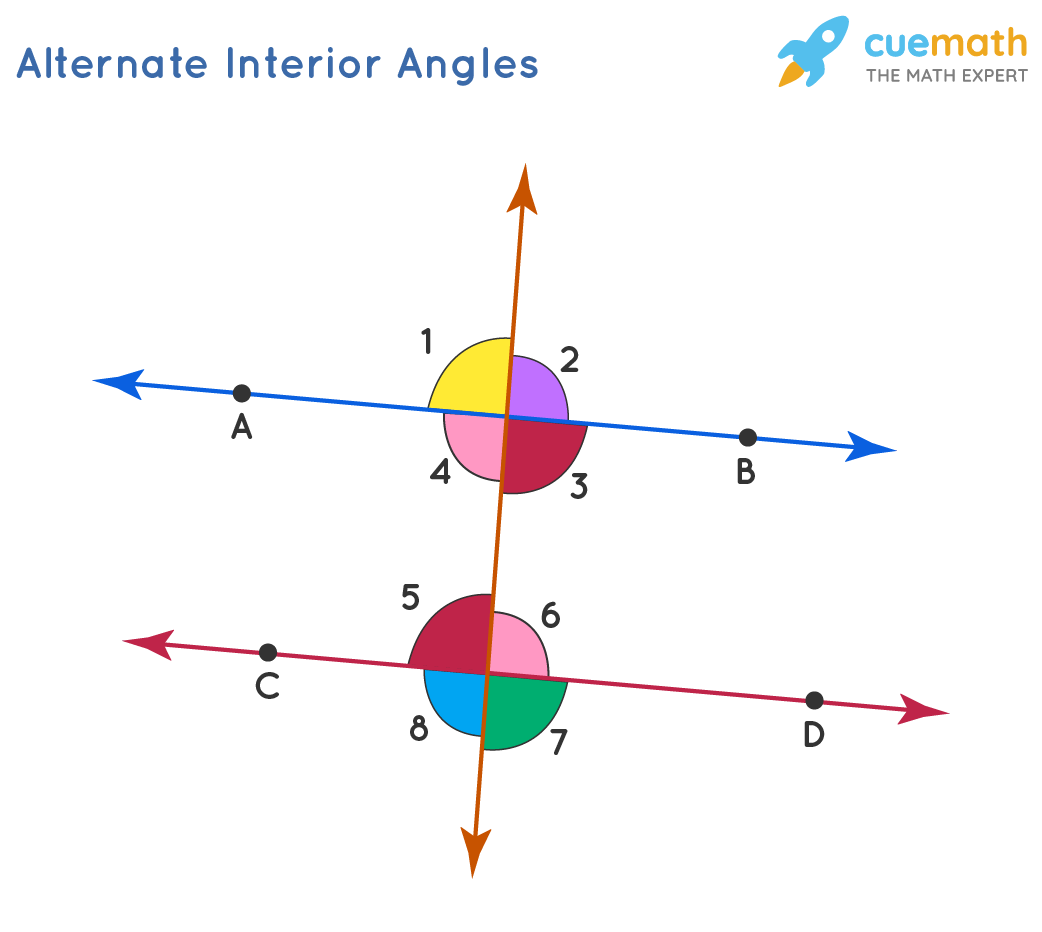
Alternate Interior Angles Definition
When a transversal intersects two parallel lines, the pair of angles created on the inner side of the parallel lines, but different sides of the transversal are known as alternative interior angles. These angles are always the same size. You can also interpret it as. The different interior angles demonstrate whether or not the provided lines are parallel. If these angles are equivalent, the provided lines intersected by the transversal are parallel.
Types of Alternate Angles
· Alternate Interior Angle
· Alternate Exterior Angle
The alternate exterior angles are ones with different vertices, located on opposite sides of the transversal, and are exterior to the lines. The alternate exterior angles generated when a transversal meets two parallel lines are always equal. The pairs of opposite outside angles in the same figure also are 1 & 7 and 2 & 8.
What is a transversal line?
A transversal line is a line that connects or crosses two other lines. When two additional lines are parallel, the transversal crosses across each at the same angle. The other two lines do not have to be parallel in order for a transversal to cross them.
What are parallel lines?
As we know parallel lines are two lines that never intersect or cross in a two-dimensional plane. When a transversal crosses over parallel lines, the generated angles have unique characteristics. These characteristics do not exist when the lines are not parallel.
Alternate Interior Angles are equal
Therefore we present to you the way to prove that Interior Angles are equal.
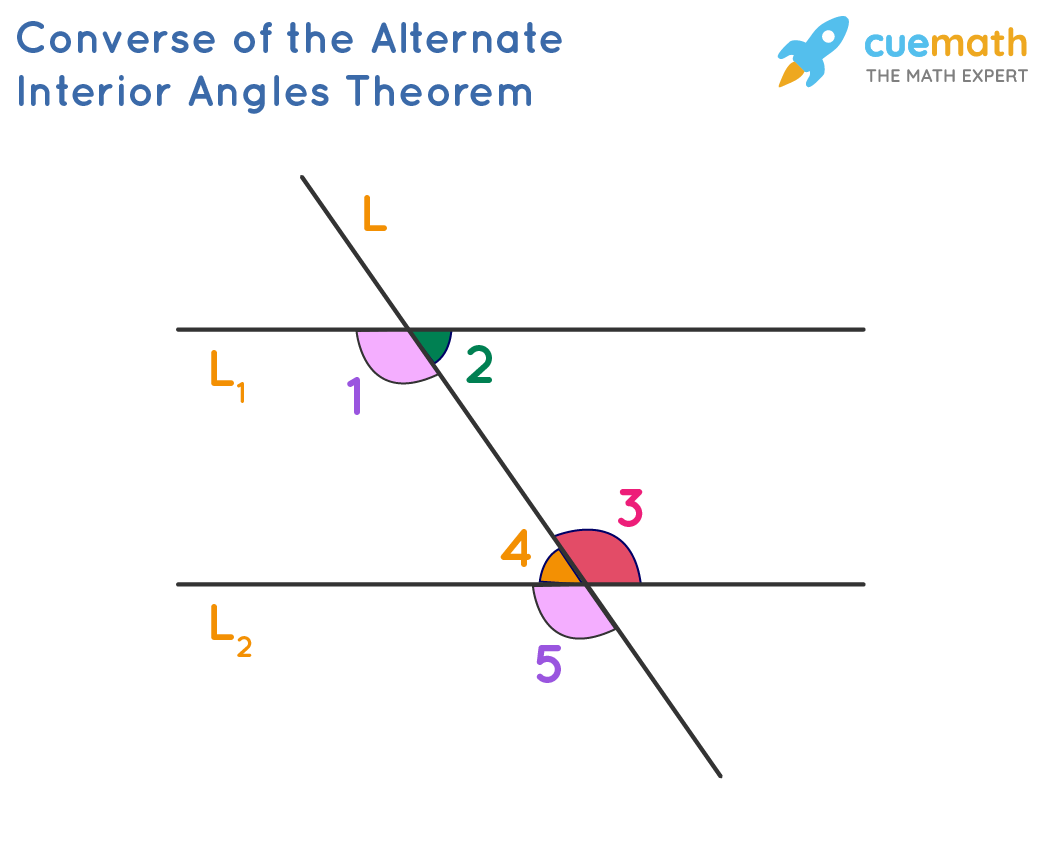
We know that if k ∥ l, then ∠2≅∠8 and ∠3≅∠5 . ,
According to the Corresponding Angles theorem,
∠1≅∠5.
Therefore, by the definition of congruent angles,
m∠1=m∠5.
Since ∠1 and ∠2 form a linear pair, they are supplementary, so
M∠1+m∠2=180°.
Also, ∠5 and ∠8 are supplementary, so
M∠5+m∠8=180°.
Substituting m∠1 form∠5, we get
M∠1+m∠8=180°.
Subtracting m∠1 from both sides, we have
M∠8=180°−m∠1 =m∠2.
Therefore, ∠2≅∠8.
You can prove that ∠3≅∠5 using the same. This theorem’s inverse is also valid. If a transversal cuts two lines k and l so that the alternate interior angles are equivalent.
How to find Alternate Interior Angles
The alternate interior angles of two parallel lines are equal, according to the alternate interior angles theorem. This information is also used to calculate alternate interior angles. Therefore, let me illustrate this with an example.
The diagram below depicts a map in which the Sixth Avenue road runs perpendicular to the adjacent First and Second Streets. Another route, Maple Avenue, forms a 40° angle with 2nd Street. But can you calculate the angle x?
The two streets are parallel, and Maple Avenue is regarded also as the transversal. Therefore x and 40° are the alternate interior angles, according to the alternate interior angles theorem. As a result, both angles are equal. As a result, x = 40°.
- Each pair of alternate internal angles has the same value.
- One co-interior angle pair is extra.
- Each corresponding angle pair is also equal.
- Each alternating pair of outside angles is equal.
The z-pattern is another technique to consider different interior orientations. It’s worth noting that a pair of alternate interior angles also forms a Z.
Alternate Interior Angles properties
- Interior angles which are opposite each other are congruent.
- The total of the angles generated on the same side of the transversal by the two parallel lines equals 180°.
- In the case of non-parallel lines, alternate interior angles have no special characteristics.
Alternate Interior Angles Theorem
According to the Alternate Interior Angles theorem, when a transversal intersects two parallel lines, the pairs of alternate interior angles are congruent.
A theorem is a proven assertion or accepted concept that has been demonstrated to be correct. The antithesis of this theorem, which is essentially the reverse, is also a proven statement. If a traversal slices two lines, and the alternate interior angles are congruent, then the lines are parallel. You can use these theorems to solve geometry issues and locate missing information. This graphic indicates which angles are equal and alternate inside. Take note of how the lines are parallel. Let us explain this with the assistance of the following diagram: 1 = 5 (equivalent angles), 3 = 5 (vertically opposite angles). As a result,1 Equals 3. Similarly, we may demonstrate that 2 Equals 4. This demonstrates how the two provided lines are parallel since their alternative inner angles are equivalent.

Alternate Interior Angles example
Example 1:
We have two angles (4x – 19)° and (3x + 16)° , they are congruent alternate interior angles. Now, Find the value of x and also find the value of the other pair of alternate interior angles,
Solution
⇒ 4x – 19 = 3x + 16
⇒ 4x – 3x = 19+16
x = 35
So, x = 350
(4x – 19)0 ⇒ 4(35) – 19 = 1210
We know angles formed on the same side of the transversal are called supplementary angles. Thus, the value of the other pair is:
⇒ 1800 – 1210= 590
Example 2:
There are two consecutive interior angles are (2x + 10) ° and (x + 5) °. Find what the angles measure.
Solution:
Consecutive interior angles are supplementary.
⇒ (2x + 10) ° + (x + 5) ° = 180
⇒ 2x + 10 + x + 5 = 180
⇒ 3x + 15 = 180
Subtracting 15 from both sides.
⇒ 3x = 165
Now we divide both sides by 3.
x = 55
Thus, the consecutive interior angles are:
⇒ (2x + 10) ° = [2(55) + 10] ° = 120°
⇒ (x + 5) ° = 55 + 5° = 60°
Example 3:
If the given angles (2x + 26) ° and (3x – 33) ° are alternate interior angles and are congruent. Find what the two angles measure.
Solution:
Alternative interior angles are equal, therefore:
⇒ (2x + 26) ° = (3x – 33) °
⇒ 2x + 26 = 3x – 33
x = 59
The measure of the angles is 144°.
Example 4:
Find the value of x when (3x + 20) ° and 2x° are consecutive interior angles.
Solution:
We know consecutive interior angles are supplementary, so
⇒ (3x + 20) ° + 2x° = 180°
⇒3x + 20 + 2x = 180
⇒5x + 20 = 180
Subtracting 20 from both sides
⇒5x = 160
Dividing each side by 8.
x = 32
So, the value of x is 32 degrees.
The consecutive interior angles are, 60° and 120°.
FAQ’s on Alternate Interior Angles
How many pairs of alternate interior angles are there in a transversal?
In a single traversal you will find two pairs of alternate interior angles.
Are alternate interior angles supplementary or complementary?
They are congruent. However, consecutive interior angles are supplementary.
What do alternate interior angles add up to?
They add up to 180 degrees.
Alternate Interior Angles on the ……. side of the transversal
Alternate Interior Angles on the different side of the transversal.
Explanation:
When a transversal meets two coplanar lines, we get alternate interior angles. Any two crossing lines must be in the same plane and hence coplanar. They are on the inside of the parallel lines but on the outside of the transversal. These angles indicate whether the two provided lines are parallel.
Read Also: Alphanumeric characters: Functions, Examples and Everything You Need to Know
When two angles share a common side and a vertex, they are said to be neighboring. When two lines meet, the angles are known as known as vertically opposite. Since one angle is opposite to the other. The alternate internal angles are congruent when a transversal crosses the collection of parallel lines. The two lines are parallel if the alternate interior angles generated by the transversal line on two coplanar are congruent. If two things have the same size and shape, they are congruent.