Functions are an extremely important part of Mathematics and Physics. In the context of functions, domain and range are two topics that we have to discuss. The domain and range calculator calculates the domain and the range of a given function.
For a function y = f(x),
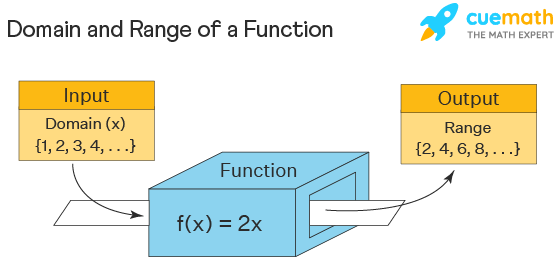
A domain is defined as the set of possible values “x” of a function that will give the output value “y”. It is the set of possible values for the independent variables. The range of a function is defined as the set of resulting values of the dependent variable. These are the set of output values when the x values are substituted. It is similar that, when the input values are given to the function, it will produce the output.
In short, a domain is defined as the set of values for which the function f(x) is defined, whereas the range is defined as the set of values that the function takes. The domain is called the replacement set, and the range is called the solution set.
Domain and range calculator:
The domain and range calculator is an online tool that is used to find the domain and range of a function.
Anyone who wishes to calculate the domain and range of a function can use the domain and range calculator.
- The domain and range calculator is very easily available on the internet.
- The process is quite simple and hassle-free.
- Gives you accurate results every single time.
- Saves time, in comparison to the pen-and-paper-based calculation method.
To summarize, the domain and range calculator is an amazing tool that can make domain and range calculations a lot easier for you.
Domain and range calculator with steps:
We can easily use the domain and range calculator to perform calculations. In fact, the procedure is also quite simple.
Follow these steps to find the correct results for the domain and range of functions:
Firstly, enter the function in the provided ‘input function’ box.
Secondly, click the ‘calculate domain and range’ button to obtain the results.
Finally, the output box will display the values of the domain and the range of the required
function.
We are providing you a link to this calculator so that the calculation becomes easier for you:
Domain and range calculator graph:
However, computing the domain and range of a function is simply not enough. Often, we have to follow this process by plotting the graph of the function. Here, we use the values of its domain and range to plot it.
Actually, this process is pretty simple. We plot the values of x on the horizontal axis and the values of y on the vertical axis.
Firstly, we have to plot the values of y that we obtain from the function, corresponding to any value of x.
Next, we join these points to form the graph of the function.
This same task can be carried out using an online calculator as well. In this case, all you have to do is to put the function in the provided space. Then, click on the ‘compute input’ button. The graph for that particular function is displayed. Further, we are providing you the link to access this calculator so that the entire process of drawing the graph becomes a lot easier:
Domain and range calculator using points:
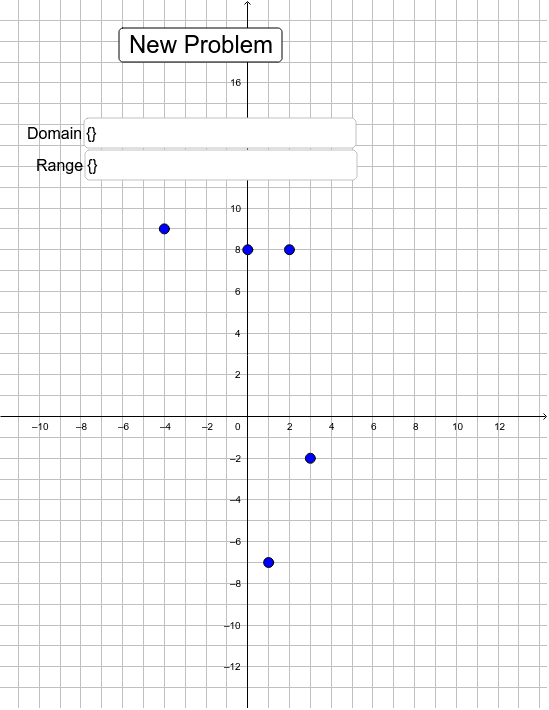
You can also find the domain and range when you have a set of points available, instead of a function. In fact, it may sound surprising at first but it is true.
Repeating what we have said before, the points are simply coordinates.
For example, consider a coordinate in the form (x, y).
The value x can be any number and the value of y is the value of the function for any corresponding value of x.
In other words, x and y are the domain and the range of the function. Since x can be any value and the value of y is dependent on the value of x, you can understand that the last statement is true.
Say, for any given set of points of a function (a,b), (c,d), (e,f) and, (g,h),
The domain of the function is: {a, c, e, g} and,
The range of this function will be: {b, d, f, h}.
Clearly, we have easily computed the domain and range of the function, given its coordinates.
Domain and range calculator Mathway:
Interestingly, the domain and range calculator is available separately on Mathway.
Find the domain calculator:
Perform the following steps to use this calculator:
Firstly, Enter the Function you want to domain into the editor.
The domain calculator allows you to take a simple or complex function and find the domain in both intervals and set notation instantly.
Secondly, Click the blue arrow to submit and see the result!
Finally, the output box displays the result.
The link for accessing this domain calculator by mathway is:
Find the domain and range calculator:
Similarly, if you want to find the domain and the range of a function together, then you can use this calculator as well.
Perform the following steps to use this calculator:
Firstly, enter the function for which you want to find the domain and range into the editor.
The domain and range calculator allows you to take a simple or complex function and find the domain and the range in both intervals and set notation instantly. This displays the graph of the particular function as well.
Secondly, click the blue arrow to submit and see the result!
Finally, the output box displays the result.
Further, we have shown the method of using the calculator, as an example for the function f(x) = x^2.
Domain and range calculator emathhelp:
The emathhelp domain and range calculator available online is actually useful. Also, it is very easy to use. So, using this is quite hassle-free.
To use this domain and range calculator by emathhelp, perform the following steps:
Firstly, enter the function in the first box.
Secondly, if it is a trigonometric function, you can also set an interval for it. For example, say 0 to pi.
Thirdly, click on the ‘calculate’ button.
Thus, the output window will now display the domain and range of the function.
Here, we are providing you the link to access the emathhelp calculator:
Domain and range of a function:
In the earlier sections, we have provided many domains and range calculators for you. Now, let us discuss the concepts of domain and range in detail.
The domain of a function is the complete set of possible values of the independent variable.
In plain English, this definition means:
The domain is the set of all possible x-values that will make the function “work” and will output real y-values.
However, there are two points that you need to keep in your mind as well:
- The denominator of a fractional function cannot be negative.
- Also, in this context, the term under a square root cannot be negative at any cost.
The range of a function is the set of its possible output values.
Domain and range of a modulus function:
The value of the modulus function is always non-negative. If f(x) is a modulus function, then we have:

This means if the value of x is greater than or equal to 0, then the modulus function takes the actual value, but if x is less than 0 then the function takes minus of the actual value ‘x’.
We can apply the modulus function to any real number. The range of the modulus function is the set of non-negative real numbers which is denoted as (0,∞) and the domain of the modulus function is R (where R refers to the set of all positive real numbers). Hence, the domain of the modulus function is R and the range is (0,∞).
Now, let us see how to plot the graph for a modulus function. Let us consider x to be a variable, taking values from -5 to 5. Calculating modulus for the positive values of ‘x’, the line plotted in the graph is ‘y = x’ and for the negative values of ‘x’, the line plotted in the graph is ‘y = -x’.
The graph of the modulus function looks like this:

Domain and range of trigonometric functions:
The domain and range of trigonometric functions are given by the angle θ and the resultant value, respectively. The domain of the trigonometric functions are angles in degrees or radians and the range is a real number. Some values are excluded from the domain and range of trigonometric functions depending upon the region where the trigonometric function is not defined.
The domain of trigonometric functions denotes the values of angles where the trigonometric functions are defined and the range of trigonometric functions gives the resultant value of the trigonometric function corresponding to a particular angle in the domain. There are three main trigonometric functions, namely sin θ, cos θ, and tan θ.
The three other trigonometric functions are sec θ, cosec θ, and cot θ.
For example, the domain and range of sine are:
We know that sine function is the ratio of the perpendicular and hypotenuse of a right-angled triangle. Thus, the domain and range of trigonometric function sine are:
- Domain = All real numbers, i.e., (−∞, ∞)
- Range = [-1, 1].
For example, the domain and range of cosine are:
We know that the cosine function is the ratio of the adjacent side and hypotenuse of a right-angled triangle. The domain and range of trigonometric function cosine are:
- Domain = All real numbers, i.e., (−∞, ∞)
- Range = [-1, 1].
For example, the domain and range of tangent are:
We know that the tangent function is the ratio of the opposite and adjacent sides of a right-angled triangle. Tan is the ratio of sine and cosine function, therefore the domain of tan x does not contain values where cos x is equal to zero.
Hence, the domain and range of trigonometric function tangent are:
- Domain = R – (2n + 1)π/2
- Range = (−∞, ∞).

Domain and range examples:
Example 1:
Find the domain of f (x) = 5x − 3
Solution
The domain of a linear function is all real numbers, therefore,
Domain: (−∞, ∞)
Range: (−∞, ∞)
Example 2:
Find the domain of the function f(x)=−2x2 + 12x + 5
Solution
The function f(x) = −2x2 + 12x + 5 is a quadratic polynomial, therefore, the domain is (−∞, ∞).
Example 3:
Determine the domain of x−4/ (x2 −2x−15)
Solution
Set the denominator to zero and solve for x
⟹ x2 − 2x – 15 = (x − 5) (x + 3) = 0
Hence, x = −3, x = 5.
For the denominator not to be zero, we need to avoid the numbers −3 and 5. Therefore, the domain is all real numbers except −3 and 5.
Example 4:
Calculate the domain and the range of the function f(x) = -2/x.
Solution
Set the denominator to zero.
⟹ x = 0
Therefore, domain: All real numbers except 0.
The range is all real values of x except 0.
Here are a few more for you to practice:

Domain and range calculator FAQs:
1. What do you mean by the domain and range of a function?
Ans: The domain of a function f(x) is the set of all values for which the function is defined, and the range of the function is the set of all values that f takes.

2. How do you find the domain and range of a quadratic function?
Ans: The values of a, b, and c determine the shape and position of the parabola. The domain of a function is the set of all real values of x that will give real values for y. The range of a function is the set of all real values of y that you can get by plugging real numbers into x. The quadratic parent function is y = x2.
3. What is the easiest way to find the range of a function?
Ans: Overall, the steps for algebraically finding the range of a function are:
Firstly, write down y=f(x) and then solve the equation for x, giving something of the form x=g(y).
Secondly, find the domain of g(y), and this will be the range of f(x).
Finally, if you can’t seem to solve for x, then try graphing the function to find the range.
On the contrary, you can also use the domain and range calculator available online to compute the domain and range of a function accurately.
4. How are the domain and range of a function related?
Ans: The domain is the set of all first elements of ordered pairs (x-coordinates). The range is the set of all second elements of ordered pairs (y-coordinates). Only the elements “used” by the relation or function constitute the range.
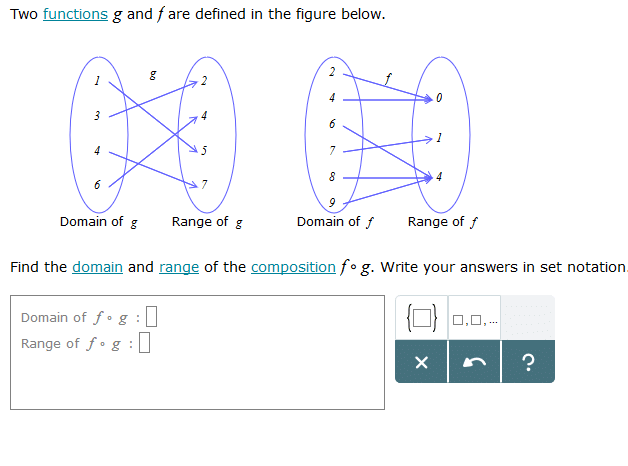
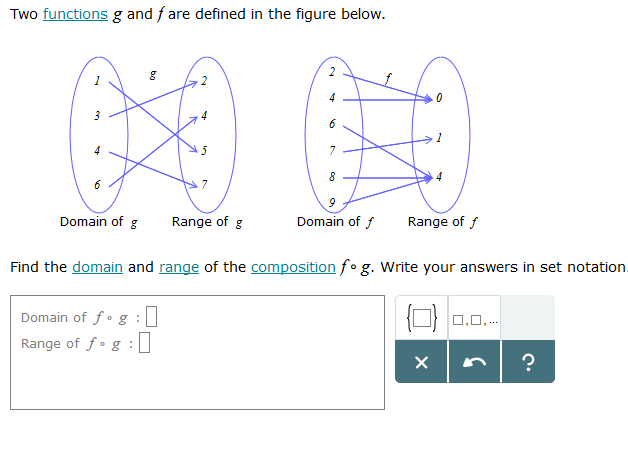
5. How do you identify the domain and range from a mapping function?
Ans: A mapping diagram consists of two parallel columns. The first column represents the domain of a function f and the other column for its range. Lines or arrows are drawn from domain to range, to represent the relation between any two elements.
6. Can I use the domain and range calculator to find the graph of a function?
Ans: Yes, you can use a domain and range calculator to even plot the graph of a function. Even though not all calculators provide this function, there are many domain and range calculators that are available online for this purpose.
Also, we have provided you with such a calculator in the above article.