If I write this mathematically then, let s be the sum of 1 cube plus two cubes plus three cubes plus four cubes up to n cube. Now there are two important things that we already know.

Now, the first thing is the sum of squares of first n natural numbers. Let’s say some s1 is one square plus two square plus three squares up to n square. Then, we will be using this result while proving the sum of the cubes of first n natural numbers. So, the result equals n times n plus one time two n plus one divided by 6. Also, let s be the sum of first n natural numbers that is one plus two plus three up to n. Next, this sum is equal to n times n plus one by two. Then, the sum of the cubes of the first n natural number is the square of s2. However, if we scale this n times n plus one by two, then we will end up getting the sum of the cubes of first n natural numbers.
Sum of cubes of n natural numbers proof
Moreover, if we write an expression that is n to the power four minus of n minus one to the power four. So, the same expression can also be written as n to the power four minus of n minus one whole square times n minus one whole square. Thus, this will be n to the power four minus of n square minus 2n plus one times n squared minus 2n plus one. Again if we expand it further, this becomes n to the power 4 minus 2n to the power three-plus n squared minus 2n to the power cube plus four n square minus two n plus n square minus two n plus one. Then will expand this again and cancel the opposite ones. Then it becomes four n cube minus six n square plus four n minus one. Hence, if we substitute the values, then it will be:
14 – 04 = 4 × 13 – 6 × 12 + 4 × 1 – 1
Next, 24 – 14 = 4 × 23 – 6 × 22 + 4 × 2 – 1
Next, 34 – 24 = 4 × 33 – 6 × 32 + 4 × 3 – 1
Now, 44 – 34 = 4 × 43 – 6 × 42 + 4 × 4 – 1
Now, n4 – (n – 1)4 = 4 × n3 – 6 × n2 + 4 × n – 1
Final step
Now let us try to interpret this, so this becomes:
n4 = 4Sn – 6 × [n(n + 1)(2n + 1)/6] + 4 × [n(n+1)/2] – n
Now, 4Sn = n4 + n(n + 1)(2n + 1) – 2n(n + 1) + n
Next, 4Sn = n4 + n(2n2 + 3n + 1) – 2n2 – 2n + n
Then, 4Sn = n4 + 2n3 + 3n2 + n – 2n2 – n
Then, 4Sn = n4 + 2n3 + n2
Now, 4Sn = n2 (n2 + 2n + 1)
Next, 4Sn = n2 × (n + 1)2
At last, Sn = [n2 × (n + 1)2]/4 which is equal to 13 + 23 + 33 + 43 + … + n3.
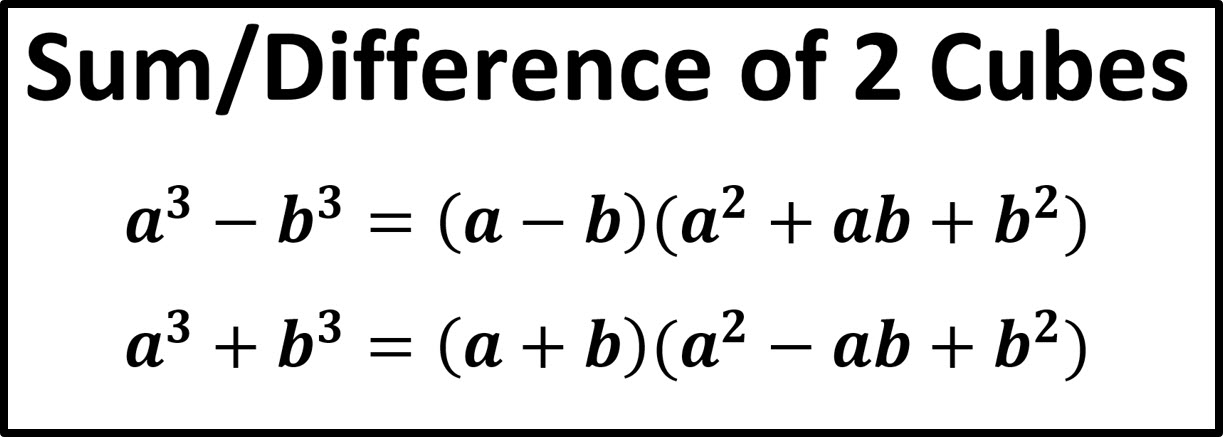
Sum of cubes of n natural numbers formula
Now, the sum of cubes of n natural numbers formula is n square times n plus one whole square upon four.
So, 1^3+ 2^3+ 3^3+ 4^3+………+n^3 = n^2(n+1)^2 /4.
Sum of cubes of 10 natural numbers
Now, one cube plus 2 cubes plus 3 cubes up to 10 cubes equals 10 multiply 11 upon 2 whole squares. Then the result is 3025.

So, 1^3 + 2^3 + 3^3 +……+ 10^3 = [10 × 11 /2]^2 = 55^2 = 3025.
Sum of cubes of binomial coefficients
Now, the sum of cubes of binomial formula is m plus n whole cube equals to m cube plus 3 times m squared times n plus 3 times m times n squared plus n cube. However, it is equal to m cube plus 3 m square n plus 3 m n squared plus n cube.
So, (m+n)^3 = (m)^3 + 3(m)^2(n) + 3(m)(n)^2 + (n)^3 = m^3 + 3m^2 n + 3mn^2 + n^3.
As an example,
(x + 2)^3 = (x)^3 + 3(x)^2 (2) + 3(x)(2)^2 + (2)^3 = x^3 + 6x^2 + 12x + 8.
Next, (2x + 5y)^3 = (2x)^3 +3(2x)^2 (5y) + 3(2x)(5y)^2 + (5y)^3 = 8x^3 + 60xy + 300xy^2 + 125y^3.
Next, (x + y)^3 = (x)^3 + 3(x)^2(y) + 3(x)(y)^2 + (y)^3 = x^3 + 3x^2y + 3xy^2 + y^3.
Sum of cubes of roots of a cubic equation
Suppose you are given a cubic equation with roots alpha beta and gamma, then asked to find a new cubic equation with the cubes of those roots. Moreover, we are going to use alpha cube plus beta cube plus gamma cubed. Remember, alpha times beta times gamma equals to minus d by a. Now alpha plus beta plus gamma whole cube equals alpha plus beta plus gamma times alpha square plus alpha-beta plus alpha gamma plus alpha-beta plus beta square plus beta-gamma plus alpha gamma plus beta-gamma plus gamma square.
Next, we need to multiply them and then cancel the opposite ones. After that, we need to take the common alpha beta and gamma. Then after some calculations, the result will be alpha cube plus beta cube plus gamma cube plus 3 times alpha-beta plus alpha gamma plus beta-gamma times alpha plus beta plus gamma minus 3 alpha beta gamma.
Sum of cubes of consecutive numbers
As an example, suppose we take three cubes. Now we can express three cubes as the sum of three consecutive odd numbers. Moreover, the first odd number is three into two plus one which is 7. Then the second and third number is 9 and 11. Next example is ten cubes. So, we can see there are 10 consecutive odd numbers present. Now, we have to find the first consecutive odd number like ten cube equals 10 into 9 plus one which is 91. Then the other odd numbers are 93, 95, 97, 99, 101, 103, 105, 107, and 109.
Now, 3^3 = 3×2+1 = 7
Next, 10^3 = 10×9+1 = 91
Sum of cubes of infinite GP
Q. The sum of an infinite GP is 57 and the sum of their cubes is 9747. Find the GP.
Ans:- So, a is the first term, and let r is the common ratio. Now, here the GP is 57. Next, that means an upon 1 minus r equals 57. Now take the cube for both sides. Then it will be a cube upon one minus r whole cube equals 57^3. Next, A cube upon 1 minus r whole cube into 1 minus r cube upon a cube which is equal to 57^3 by 9747. Now we need to cancel a cube. Then it will be 1 minus r cube by 1 minus r whole cube is equal to 19. Now, 1 plus r plus r square upon 1 minus r whole square equals 19.
Thus we need to solve this. 1 plus r plus r square equals 19 plus 19 r square minus 38 r. Now we get 18 r square plus 18 minus 39r. Next, we need to factor it in. In this factor, 3r minus 2 into 6r minus 9 are distributed which equals 0. Hence, in this equation, we get the value of r which is 2 by 3. Therefore we put the value of r and it will be an upon 1 minus 2 by 3 equals to 57. At last, we get the value of a which is 19. Now, GP equals 19, 38/3, 7c/9, 152/27,……, infinity.
Sum of cubes examples
Example 1
- Use the sum of cubes formula to find the factor of 216×3 + 64.
- At first we are using the sum of cubes formula to determine the factor of 216×3 + 64.
Now, (6x)3 + 4^3 = 216x^3 + 64
So, Using the formula for the sum of cubes,
(a + b)(a^2 – ab + b^2) a^3 + b^3 = (a + b)(a^2 – ab + b^2)
Now, Place the values in the appropriate places.
(6x + 4) ((6x)^2 – 6x × 4 + 4^2)= (6x)^3 + 4^3
Next, (6x+4)(36x^2 – 24x +16)= (6x)^3 + 4^3
Next, 8(3x+2) (9x^2 – 6x +4)= (6x)^3 + 4^3
At last, 2(3x + 2)(9x^2 – 6x + 4) is the factor of 216×3 + 64.
Example 2
- Find the factor of 8×3 + 125y3.
- Using the sum of cubes formula, determine the factor of 8×3 + 125y3.
Now, (2x)^3 + (5y)^3 = 8x^3 + 125y^3
Next, Using the formula for the sum of cubes,
(a + b)(a^2 – a^b + b^2) = a^3+b^3
Now, Place the values in the appropriate places.
(2x)^3 + (5y)^3 = (2x + 5y)((2x)^2 – (2x)(5y) + (5y)^2)
So, (2x)^3 + (5y)^3 = (2x + 5y)(4x^2 – 10xy + 25y^2)
At last, (2x + 5y)(4x^2 – 10xy + 25y^2) is the factor of 8x^3 + 125y^3.
Example 3
- Simplify 193 + 203 using the sum of cubes formula.
- To determine the sum of 19^3 and 20^3, we are using the sum of cubes formula.
Now, assume that a = 19 and b = 20.
So, a^3 + b^3 = (a + b) (a^2 – ab + b^2)
Moreover, We’ll use the formula a^3 + b^3 = (a + b) (a^2 – ab + b^2) to replace them in the a^3 + b^3 formula.
Next, (19+20)(19^2 – (19)(20)+20^2) = (39)(361-380+400) = (39)(381) = 14,859.
At last, 14,859 is the answer of 19^3 + 20^3.
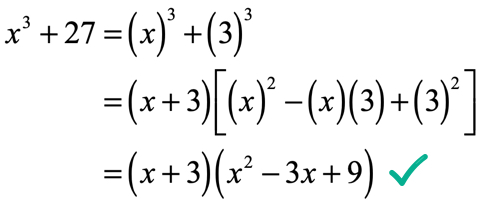
Some frequently asked questions
What is the sum of cube numbers?
So, (n(n+1)/2)2 is the sum of cube numbers.
What is the sum of cubes formula?
So, a3 + b3 = (a + b) (a2 – ab + b2) is the sum of cubes formula.
What is the summation of n?
So, S=n(n+1)2 is the summation of n.
What is a cube of a number?
So, a cube number is a number that has been multiplied three times. Moreover, this is also known as a ‘number cubed.’ 3 is the sign for cubed. As an example, 4^3 = 4 ×4 ×4= 64.
What is the sum of the cube of the first 7 natural numbers?
So, 19.316088 is the sum of the cube of the first 7 natural numbers.
Why is the sum of cubes square of sum?
However, we investigate, for each n, the Diophantine equation expressing all non-trivial sets of n integers with this feature, which is inspired by the fact that the total of the cubes of the first n naturals is equal to the square of their sum.
What is the sum of n odd numbers?
So, n^2 is the sum of n odd numbers where n is a natural number.
What is the sum of n 3?
Even though it appears that the total is always square, the sum of the first n cubes, 13+23+… + n 3 = (n (n +1)/2)2, which is the square of the nth triangular number, is surprising. Now, 13+23+… +103=(10111/2)2=552 = 3025, for example.





