The equation of a circle calculator is a free tool that people use online. This application gives us the equation of a circle for any input that we feed. There are many different sites that give free equations for circle calculators.
When students use these tools, it is not only more efficient and accurate, it also gives fast results. Thus we can obtain the equation of a circle using the equation of a circle calculator in just a few seconds. Keep reading to find out more about the different mathematical equations of a circle and how to derive and use them.

How to Use the Equation of a Circle Calculator?
Many people struggle with using the equation of a circle calculator efficiently. Many times they get confused about the parameters and the workings. If you are trying to find out how to use the equation of a circle calculator then you don’t have to look any further. Here is a simple way in which you can use the equation of a circle calculator:
Firstly, you have to type the radius of the circle and the center of the circle. You will be able to see the corresponding fields in the equation of a circle calculator. Thus you have to enter the input there correctly. If you do not put the correct numbers in the equation of a circle calculator the answer will be incorrect.
Next, you have to click on the Find Equation of Circle button. When you click on this button you will be able to obtain the equation of a circle. Finally, the equation of a circle calculator will display the equation of a circle according to the input you have entered. They will display the output in a new window. They may even display the geometrical figure of the circle. Thus, you will get faster and more accurate results with the equation of a circle calculator.
Circles have a standard algebraic equation we have given as follows.
(x-h)² + (y-k)² = r². According to this equation, the radius of the circle is r. Thus this equation also gives the coordinates of the center of the circle. They are (h, k). Here x and y are the two axes in the graph, the x-axis, and the y axis.
What is a circle?

The most important thing to understand when we are trying to find out the equation of a circle is the definition of a circle itself. So we must discuss what a circle is first. This will help us to understand the equation of the circle better. When we have a set of points equidistant from a given plane we call it a circle.
In other words, all the points in a circle will be equally spaced from a point in a fixed plane. Thus, this fixed point from which all the points in the circle are equidistant is called the center of the circle. The letter r is the letter that we use to denote the radius of the circle. The radius of a circle is the distance between any point on the circumference of the circle and the center.
Thus, we can see that there can be two forms of the standard equation of a circle. There is the standard equation of a circle where the center of the circle occurs at the origin. There is also the standard equation of a circle whose center does not occur at the origin. In this article, we will discuss the equation and examples of the equation of a circle of both standard equations of a circle.
What is the Equation of a Circle?
The circumference of a circle is the distance between all the points on a curve from a fixed point and all the points on that curve. Thus, this fixed point is also known as the radius of the circle. Thus let us assume a circle exists whose center is (h, k). This circle has a radius of r. Thus it will have the equation (x-h)² + (y-k)² = r²
In other words, if we know the coordinates that make up the center of a circle and also its radius, then we can easily use these values to find the equation of a circle.
For example: Let us assume that the center of a circle lies on the point (1, 2). The radius of the circle is 2 cm. Thus if we calculate the equation of this circle we get the expression x minus the x coordinate squared and added to y minus the y coordinate squared. This expression is equal to the square of the radius of the circle.
Thus the final equation is: (x-1)²+(y-2)² = 2²
(x²−2x+1)+(y²−4y+4) =8
x²+y²−2x−4y-3 = 0
Is the Equation Of Circle a Function?
Many students are confused about whether a circle can be considered a function or not. However, according to algebra circles should not be functions. A function has values denoted from only a single point in the codomain. Since the line will intersect the circle at two given points we cannot consider a circle to be a function.
We can describe circles using mathematical equations. This has a lot of applications in the field of physics and applied mathematics. Thus there are many ways in which we can express the equation of a circle. The most common out of the methods is the standard and general form of the equations of a circle.
Equation of a Circle given center and radius
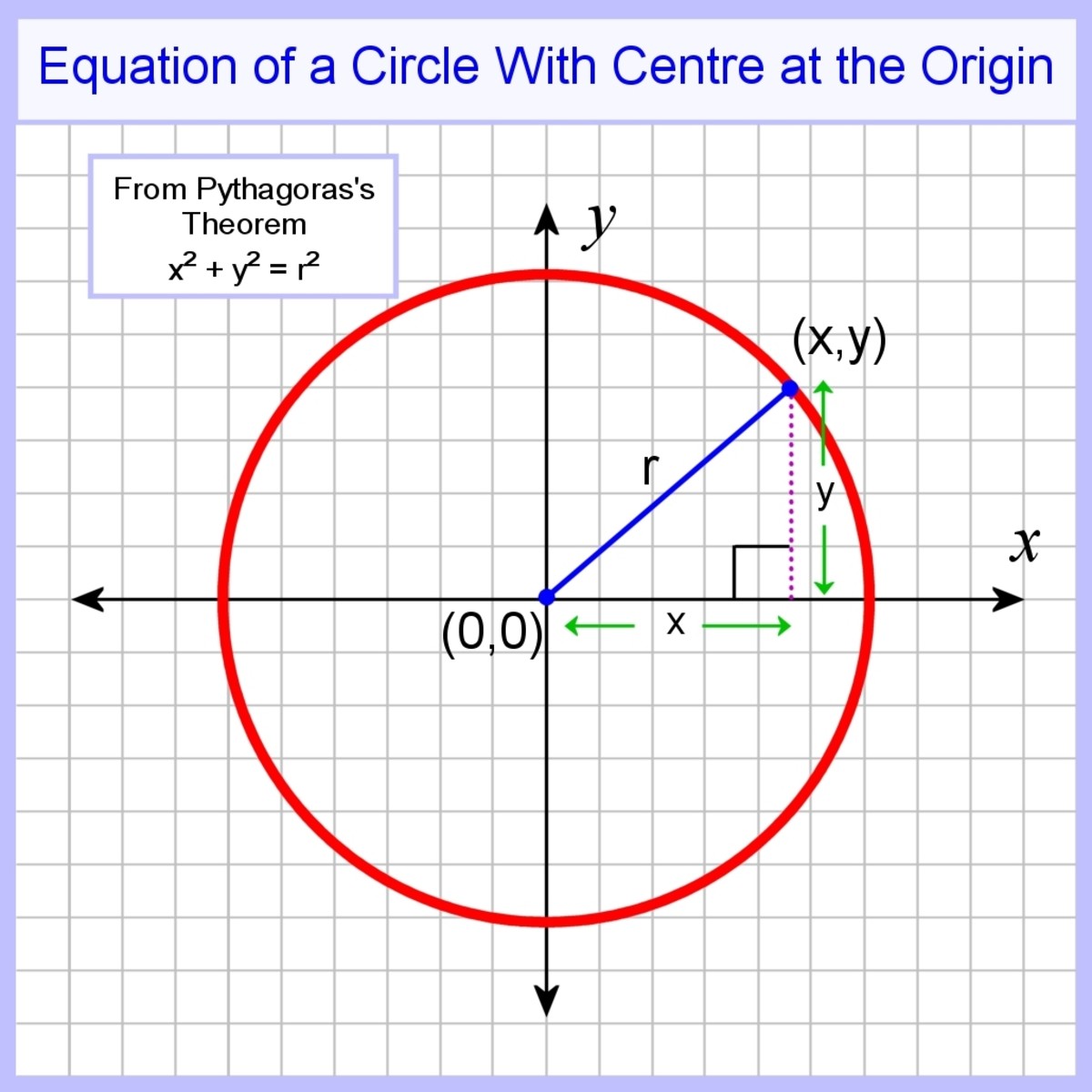
Let us consider an arbitrary point P(x, y) on the circle. Let ‘a’ be the radius of the circle that is equal to OP.
We know that we can calculate the distance between the point (x, y) and the origin (0,0) using the distance formula, which is equal to
√[x²+ y²]= a
The equation of a circle where the center coincides with the origin is:
x²+y²= a²
Where “a” is the radius of the circle.
Alternative Method
We can derive this same equation using another method. Thus, let us first assume that (x, y) is a point in a circle. We will also assume that the center of the circle is (0, 0). Then we have to imagine a right-angled triangle where the hypotenuse is formed by a perpendicular line from point x to the x-axis.
Thus, the base of this triangle will be the distance along the x-axis. The length along the y-axis is going to denote the height. Finally, we can apply Pythagoras’ theorem of right-angled triangles to solve this question. We will follow the following equation: x²+y² = (radius)².
Equation of a Circle center and a point
C(h, k) represents the center of the circle, and P(x, y) represents any point on the circle.
Therefore, the radius of a circle is CP.
By using distance formula,
(x-h)² + (y-k)² = (CP)²
Let radius be ‘a’.
In this case, the equation of the circle with center (h, k)and radius ‘a’ is,
(x-h)²+(y-k)² = a²
which is called the standard form for the equation of a circle.
General form of the equation of a circle
We can represent the general equation of any type of circle as:
x² + y² + 2gx + 2fy + c = 0, for all values of g, f and c.
If we add g2 + f2 on both sides of the equation it will give,
x² + 2gx + g²+ y² + 2fy + f²= g² + f² − c
Let us consider this equation to be equation (1)
Since, (x+g)² = x²+ 2gx + g² and (y+f)² =y² + 2fy + f² we will substitute the values in equation (1). Thus, we will have
(x+g)²+ (y+f)² = g² + f²−c
We will consider this equation to be equation (2)
When we compare (2) with (x−h)² + (y−k)² = a², where (h, k) is the center and ‘a’ is the radius of the circle, we will get:
h=−g, k=−f
a² = g²+ f²−c
Thus,
x² + y² + 2gx + 2fy + c = 0, will represent the circle with centre (−g,−f) and radius equal to a² = g² + f²− c.
If we consider g² + f² > c, then the radius of the circle is real.
If we consider g² + f² = c, then the radius of the circle is zero. This tells us that the circle is a point that coincides with the center. Such a type of circle is called a point circle.
Finally when g² + f² <c, then the radius of the circle becomes imaginary. Therefore, it is a circle that will have a real center and an imaginary radius.
How to Find the Equation of the Circle?

There are two cases in which we will need to find out the equation of a circle. The first one is when the center of the circles lies on the origin and the second one is when the center of the circle does not lie on the origin. We have included some problems to find the equation of a circle in both these cases for your benefit.
Example 1: Let us assume a circle whose center is at the origin and whose radius is 2.
Solution:
According to the problem, the center is (0, 0), and the radius is 2 units.
We know that the equation of a circle when the center is origin is
x²+ y² = a²
For the given condition, the equation of a circle is given as
x² + y² = 2² implies
x² + y²= 4, which is the equation of the required circle
Example 2: Write down the equation of the circle whose center is (3,5) and whose radius is 4.
Solution:
Since the center of the circle is not an origin in this problem, the general equation of the circle is,
(x-3)² + (y-5)² = 4²
x² – 6x + 9 + y² -10y +25 = 16
x² +y² -6x -10y + 18 =0 which is the final equation.
Example 3:
The equation of a circle is x²+y²−12x−16y+19=0. Find out the center and radius of the circle.
Solution:
According to the question the equation is of the form x²+ y² + 2gx + 2fy + c = 0,
2g = −12, 2f = −16,c = 19
g = −6,f = −8
Thus, the centre of the circle is (6,8)
We can calculate the radius of the circle as = √[(−6)² + (−8)² − 19 ]= √[100 − 19] =
= √81 = 9 units.
Thus, the radius of the required circle is 9 units.
Important points on Equation of Circle calculator

There are a few things we need to keep in mind when we are calculating the equation of a circle. These points will help us to avoid errors and solve problems faster and more efficiently.
Thus, we must always remember that the standard form of the equation of a circle always has x² + y² in the beginning.
If a circle crosses two axes y and x, then it will have four points at which it interacts with those axes.
A circle that touches both axes x and y will have only two points of contact with them.
If there is an equation that is in the form x²+ y²+ axy + C=0, then it is not the equation of the circle. The equation of a circle usually does not have a xy term.
We always represent the equation of a circle in the polar form as r and θ. Here r stands for radius and θ represents the angles.
The radius of a circle is the distance between the center of the circle and any point on its circumference. Thus, in other words, the radius of a circle is always a positive value.
Frequently Asked Questions About Equation Of A Circle Calculator
What is the equation for a circle?
The equation for a circle is: (x-h)²+(y-k)² = a², In this formula (h,k) is the center of the circle. Thus, a is the radius of the circle.
What are the formulae of circles?
The circumference of a circle is equal to 2 (pi) of radius. Thus it can also be equal to pi of diameter. The area of a circle is equal to the square of its radius. Thus the area of a circle that has the radius r will be (r)²
What is the equation of a circle when the center is at the origin?
Since the value of coordinates is (0,0) at the origin, thus the equation of circle will be:
(x-0)² + (y-0)² = r² which implies
x² + y² = r²
If (x-6)²+(y+1)²=9 is the equation of a circle, then what is the center of the circle?
According to the problem, (x-6)²+ (y+1)² =9 is the equation of a circle. If we compare this equation with the standard equation, we will get:
(x-h)²+(y-k)² = a²
h=6 and y = -1
Therefore the center of the circle asked in the question will be (6, -1)
How do we know if an equation is the equation of a circle?
If x and y are squared in the equation and the coefficient of x² and y² are the same, then we can assume that it is an equation of the circle. This is because the standard equation of a circle follows the general structure of x squared and added to y on one side and radius squared on the other side. For example, x²+y² = 9 is the equation of a circle.





