So, what do you think radius means? Have we not heard this term all our lives? Well, it is a straight line that connects the center of a circle or sphere to the circumference. Or in other words, radius of a circle is the distance from its center to the outer edge. Subsequently talking of convergence, what do you think it is? To simplify, convergence occurs when two or more things, ideas, etc. become similar or combine into one. But, right now, since our topic of concern is the radius of convergence, let us make it easy for you. Hence, we need to apply the term in its mathematical sense. In maths, the radius of convergence refers to the distance in the complex plane. Moreover, the calculation occurs between the expansion point and the nearest singularity of the expanded function.
The Radius of Convergence Calculator is a free online tool that displays the point of convergence for a given series. Many websites offer an online radius of convergence calculator that speeds up results. Besides, such calculators also give you the convergence point in a matter of seconds.
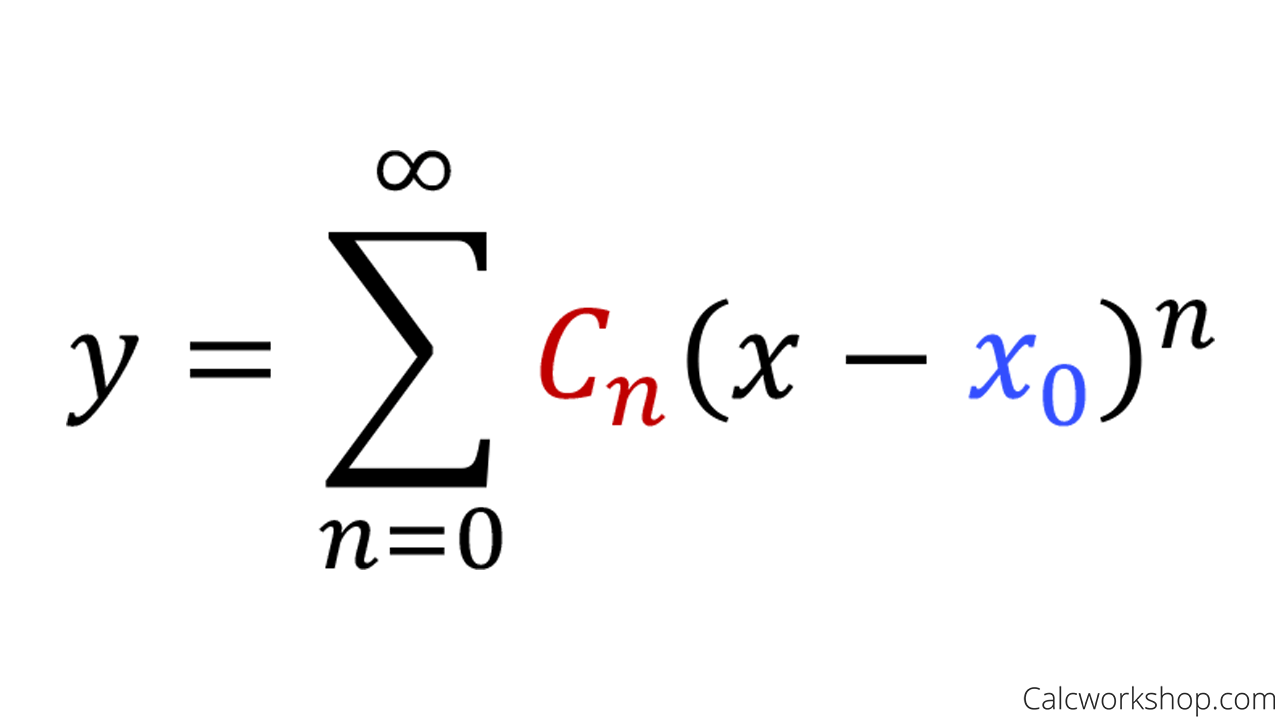
Image Credit – CWS
If you would like to know more about the radius of convergence calculator of a series, then worry not. You have landed on the correct site. This article will also show you all of the steps to manually solve the radius of convergence calculator. Besides, we shall list down a few examples for you too. Scroll over to read more.
Radius of Convergence Calculator Wolfram
The following show the steps, as to how you should use the radius of convergence calculator. Wolfram is one of those famous radiuses of convergence calculators.
1st Step: Fill in the necessary input fields with the function and range.
2nd Step: Further, to obtain the result, click the ‘Calculate’ button.
3rd Step: Finally, in the new window, you will see the display of the convergence point for the definite series.
Radius of Convergence Calculator Power Series
It is now time to look at some specific types of series. Slowly, we shall get to the stage where we can cover a handful of series exercises.
We shall now bring up the power series. The fact that a power series is a function of x is the first thing to notice. We usually do not come across such types of series. In general, we allow integers in the series, but now we’re letting variables in the series too. However, this is not going to have any effect on how things are done. All that we know about the series holds true. The only change is that the values of x we shall enter now will drive the series’ convergence. For some x values, a power series may converge, whereas for others, it may not.

Well, it is the radius of the greatest disk at the series’ center, where it converges. The radius of convergence of a power series is either a positive or negative real number or infinity. When positive, the power series converges entirely and uniformly. It does so on compact sets inside the open disk of radius equal to the radius of convergence.
The radius of convergence is the shortest or minimum of all the respective distances (which are all non-negative numbers). We should calculate it from the center of the convergence disk to the respective singularities (multiple) of the function. If you are not familiar, singularities are those values of the argument for which you cannot define the function. At singularity, any function takes an infinite value.
Radius of Convergence Definition
How do you think mathematicians define the radius of convergence? We know that the power series will converge at its Center of Convergence at some point. The distance between the center of convergence and the other end of the interval becomes the radius of convergence. We can use the ratio test to calculate the radius of convergence of a power series. This test, which tells us how to find the limit, is the best way to find convergence. This test checks the convergence point if the limit is smaller than one.
Radius of Convergence Calculator Root Test
The root test is a criterion for an infinite series’ convergence (a convergence test) in mathematics. Likewise, it is conditional on the quantity. From geometric series to more general series, it carries over logic. In addition, it states that the series converges absolutely if this quantity is less than one. However, it diverges if it’s of use while dealing with power series.

Augustin-Louis Cauchy was the first to design this root test. Subsequently, he published it in his textbook Cours d’analyse (1821). As a result, it is also famous as the Cauchy root or Cauchy’s radical test.
Radius of Convergence Calculator with Steps
To find the radius of convergence of a power series, follow these simple steps.
- Take a look at a power series.
- Consider what x value will cause the power series to converge.
- Subsequently, find the radius of convergence by doing a ratio test.
- Further, use the ratio test to size up the function.
- Likewise, act on the limit value by using a ratio test.
- To get the R or Radius of Convergence, replace or substitute the limit value.
Likewise, there are two cases that arise. The first one is fully theoretical though. Here, you take specific limits and find the precise radius of convergence after you know all the coefficients Cn. On the other hand, the second one is more practical. While building a power series solution to a taxing problem, you will often only know a finite number of terms. And these terms in a power series range from a few to a hundred. Setting down a plot can roughly guess the radius of convergence in this second case.
Theoretical Radius of Convergence Calculator
If you use the root test to check the terms of the series, you will get the radius of convergence. As per the root test, if C<1, then the series will converge. On the other hand, if C>1, the series will diverge. Hence, if the distance between z and the center a is less, the power series converges. The Cauchy-Hadamard theorem states that if the distance exceeds that number, it diverges.
The ratio test’s limit is usually easy to find. Likewise, the presence of that limit tells you that the radius of convergence is finite.
Practical Radius of Convergence Calculator
We are only aware of a finite number of coefficients Cn usually in scientific applications. As n grows larger, these amounts usually settle into a likely pattern specified by the nearest radius-limiting singularity. The coefficients of a Taylor series are always mounting with the ratio of 1/r. Here, r is the radius of convergence.
Radius of Convergence on the Boundary
The set of all points such that it becomes a circle refers to the boundary of the disc of convergence. It takes place when the power series expands around point a and the radius of convergence is r. A power series may diverge at all points on the border, diverge at some places. However, it will converge at others, or converge at all points on the boundary. Further, even if the series converges everywhere (uniformly) on the boundary, it does not imply that it converges absolutely.
Rate of Convergence
Consider expanding the function around the point x = 0. You will discover that this series’ radius of convergence is infinity, meaning that it converges for all complex numbers. However, while solving sums, one often wants the precision of a numeral answer. Likewise, both the number of terms and the value at which you are rating the series affect the answer’s accuracy. For example, suppose you want to calculate sin(0.1) to 5 decimal places. So, you will just be needing the first 2 terms of the series. However, assess and add the first 5 terms of the series to get the same precision for x = 1. Gauge the first 18 terms of the series for sin(10), and the first 141 terms for sin(100).

Henceforth, for these certain values, the fastest convergence of a power series expansion occurs in the center. As you start moving away from the center, the rate of convergence slows. This carries on until you hit the boundary (if one exists) and cross over, at which point the series diverges.
Interval of Convergence
The interval of convergence is the range of x values for which the Taylor series converges to the function’s value. Beyond the domain, however, the Taylor series is either undefined or does not relate to the function. Thus, the radius of convergence is half the interval’s length. Furthermore, the radius of the circle within the complex plane where the series converges.

We can determine the convergence in several ways. Nevertheless, the ratio test tends to give an immediate answer for the radius of convergence, r. Test the value of the series at the endpoints -r and r. Further, use that to calculate the convergence interval. Remember, for simple functions, 1 and infinity are common radii of convergence.
Radius of Convergence Calculator Example
Let’s find the Radius of Convergence for the power series.
Sigma n = to infinity 2n / n * (4x – 8)n.
Now, to find that,
Let us take Cn = 2n / n * (4x – 8)n.
However, this power series will converge for x = 2.
Thus, the ratio test for the above power series will be:
L = (Cn + 1)/Cn.
L = lim n to infinity 2n + 1 (4x-8)n + 1/n +1 * n / 2n * (4x-8)n.
lim n to infinity 2n * (4x-8) / n + 1.
(4x-8) lim n to infinity 2n / n+1 = 2(4x-8).
So, we can obtain the following convergence data:
2(4x-8)<1.
x-aR.
8(x-2)<1.
(x-2)<⅛.
8(x-2)>1.
(x-2)>1/8.
Therefore, the radius of convergence for the power series is R = ⅛.
Radius of Convergence Calculator FAQs
What is the radius of convergence?
A: The radius of convergence is half the interval’s length. Likewise, we can also refer to it as the circle’s radius within the complex plane where the series converges.
Why do we call it ‘the radius of convergence’?
A: Mathematicians like to plug in complex values like X = U + iV, where i * i = -1. They can show that U2 + V2 = R2 converges inside the circle but diverges outside it. Hence the term – radius of convergence.
What is the radius of convergence for a Power Series?
A: Assume a power series that only converges for x = a. In this case, the radius of convergence R = 0 and the interval of convergence x = a.
What is the radius of convergence for a Geometric Series?
A: The radius of convergence R = 0, if a power series converges solely for x = a. On the contrary, the radius of convergence R = ∞, if the power series converges for all values of x.
What is the radius of convergence for a Hypergeometric Series?
A: A Hypergeometric Series is the sum of a series where the solid coefficients’ ratio k is k’s rational function. If the series is convergent, it will define a hypergeometric function. Therefore, we can form this via analytic keeping up over a larger domain of the variable.
What is the radius of convergence for a Taylor Series?
A: Put up the inequality since the ratio test states that the series will converge when L<1. Thus, the radius of convergence is R = 3 since the inequality is in the form |x-a| < R|x-a| < R.
What is the radius of convergence for a Maclaurin Series?
A: Checking which of the cases we are in will show the radius of convergence for a Maclaurin Series. Therefore, the radius of convergence R = ∞ if our Maclaurin Series converges for all real values of x.
Can the radius of convergence be zero?
A: The distance between the convergence interval’s center and the endpoints of a power series is the radius of convergence. Thus, if the series only converges at one point, the radius of convergence can be zero.
Is the radius of convergence always positive?
A: When positive, the power series converges absolutely and uniformly on compact sets inside the open disk of radius. Additionally, this radius equals the radius of convergence.
Can the radius of convergence be negative?
A: No. The very focus of Radius of Convergence shows that it is a non-negative real number or infinity.
Can the radius of convergence be infinity?
A: Well, yes. This is possible. Suppose you have a series that converges for only x = c. Hence, you can say the radius of convergence is 0, i.e., R = 0. Besides, if that series converges for all x, you can say the series has an infinite radius of convergence. In other words though, R = ∞.
Why do we need the radius of convergence?
A: We need the radius of convergence to find the interval of convergence. The radius cites the number of values at which the series converges. On the other hand, the interval gives the exact values at which the series converges and does not.
What is convergence?
A: Convergence literally refers to the union of two or more things, evolving into one. In maths, however, one can define convergence as some property of reaching a limit more closely. We can actually achieve convergence as a variable of the function increases or decreases. Likewise, a rise in the number of terms of the series also helps us to find convergence.
How can you test for convergence?
A: The following shows the conditions to test for convergence:
- The limit of a[n]/b[n] is positive. – The sum of a[n] converges if and only if the sum of b[n] converges.
- The limit of a[n]/b[n] is zero. – When the total of b[n] converges, the sum of a[n] converges as well.
- a[n]/b[n] has an infinite limit. – If the total of b[n] diverges, then the sum of a[n] diverges too.
What is the convergence of sin x?
A: Sine function is periodic and non-constant in nature. Henceforth, it does not converge to any value as it goes up to infinity.
What is the convergence of cos x?
A: Cosine function is even and symmetric in nature. Henceforth, it is absolutely convergent for all values of x that belong to R.
What is the convergence of tan x?
A: As x approaches infinity, tan x swings between plus and minus infinity. Meanwhile, it takes every value in between an infinite number of times. Since x tends to infinity, a function of x doesn’t require convergence to a finite limit or tend to infinity.





