The superposition theorem is based on the superposition principle which is used to analyze networks in electrical circuits. It is essential because it operates in the process of converting any circuit to either its Norton correspondent or its Thevenin equivalent.
This theorem is functional for any linear networks which might be time-varying or time-invariant. They may contain sources that are independent or linearly dependent. It also works for linear passive elements like resistors, inductors, and capacitors as well as for linear transformers.
Superposition theorem makes use of current and potential, but not of power. So, this means that the sum which the observer gets from the power of a single source while no current passes through the other sources is not the value of the real absorbed power. To find the power, we use the superposition theorem. We find the current and voltage of each linear element at first. Following this, we calculate the total of the average currents and potentials.
However, this theorem can calculate the average or active power under a certain case when the linear network is slowly attaining stability. In this case, each external independent source has a unique frequency. If at least two such sources have the same frequency, the superposition theorem cannot calculate the average power.

What is the definition of the Superposition Theorem?
The theorem states-
“If more than one source acts together in an electric circuit, then the current through any one of the arms of the circuit is the addition of currents which would flow through the branch for each source, keeping all the other sources dead.”
When one wants to calculate how much an individual source contributes to the power of the circuit, the other sources must have 0 potential. So, they must not exist or function in the circuit. When one moves or removes the voltage source, its value becomes null. To achieve this, one has to replace the source of the current with an open circuit. No current flows through an open circuit.
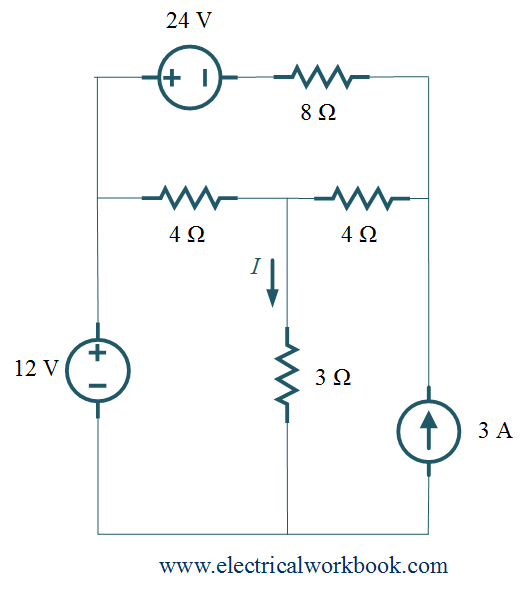
What are the conditions you need to remember to apply the superposition principle?
When one is calculating the potential, current, or power of a single source, one must be very cautious in assigning the signs to each quantity. A sign, positive or negative, is extremely important. It shows the direction in which the unknown quantity should operate. If each source has the overall circuit direction as its own, then it will have a positive sign in the sum calculation. If, on the other hand, it has the opposite direction, then it will have a negative direction in the sum calculation.
The theorem is valid for only circuits with linear independent sources. One can find currents and voltages using it.
However, one must note that the superposition theorem cannot directly find out the power of each source. This is because power does not function in the way of a linear abundance.

How to apply the Superposition Theorem?
One needs to strictly follow a few steps to apply this theorem
- There are multiple sources in the linear network of the electrical circuit. One has to choose one single source at first which one wants to find out.
- On selecting one source, one should replace every other source. No other source should exert a potential difference.
- Now, one has to undertake the approach of simplifying networks. So, one selects a particular segment of the circuit. He should then find out the amount of current passing through that part of its potential difference.
- Now, the observer has to repeat this process individually for every single source in the circuit.
- So, one should now get what each independent source contributes to the entire circuit. Following this, he has to sum up all the individual values of each factor. This should ideally give the total amount of current passing through the entire circuit or its overall voltage drop.
Prerequisites for the Superposition Theorem
By now, it must be quite clear that there are several issues you need to remember if you want to apply the superposition theorem. First of all, no matter how complex the circuit is, one must be able to reduce it in the form of series and parallel connections. Each source of power must come under it. So, by that, if the circuit is an unbalanced bridge circuit, you cannot apply this theorem. Moreover, the theorem works for no values with mathematical roots or powers. It works only with linear equations with elemental values.
We already know that this theorem can only help in determining voltage or potential and current. It cannot determine power. This is what the precondition of linearity states. This is because power dissipations are mathematically nonlinear functions. When only one independent source operates in the process, they do not algebraically add to form a whole number total. The total that the observer obtains is not accurate. Since linearity is a prerequisite, the theorem cannot work for circuits where current flow or potential differences constantly change the resistance of one or more sources or components. So, this theorem can never analyze incandescent or gas-discharge bulbs or varistors or such other components which the network accommodates.
Read Also: Ammonia – a Lewis Acid or a Lewis Base?
Moreover, one significant feature of this theorem is that all sources and components should necessarily be bilateral. This means that the direction in which electrons flow inside them does not affect them in any way. They continue operating irrespective of the direction. The polarity does not specifically matter to the working of a resistor. Therefore, all the circuits which we have considered till now adhered to this principle.

Is it possible to apply the superposition theorem to an AC as well as DC connection?
This theorem can apply itself to analyze circuits that have alternating current or AC, which have semiconductor amplifiers that generally blend or superimpose AC with DC or direct current. This is because DC is linear. Similarly, AC voltage and Ohm’s Law calculating current equations also need linearity. Therefore, superposition can analyze a circuit primarily with only the DC source of power. Next, it can analyze the AC source. Now, the results which the observer obtains can determine what will happen to the AC and the DC source in combination. So, this means there will be several consecutive equations. The observer has to solve all of these to analyze the complete electrical circuit.





